


Today position measurements are so accurate that an ellipsoid must be used. However, the precise values of the ellipsoid ( a and f or a and b ) were hard to measure. Therefore different ellipsoids were generated in different parts of the world and even in different countries close to each other.
A table with a few of the ellipsoids in use today or for maps that are still available is given below. There are about twice this many that have been used. Several ellipsoids are used in more than one datum.
Ellipsoid Name |
Semi-Major Axis (km) |
Semi-Minor Axis (km) |
1/Flattening |
|
Airy |
6377.563 |
6356.257 |
299.32 |
|
Australian National |
6378.160 |
6356.775 |
298.25 |
|
Bessel 1841 |
6377.397 |
6356.079 |
299.15 |
|
Clarke 1866 |
6378.206 |
6356.584 |
294.98 |
|
Clarke 1880 |
6378.249 |
6356.516 |
293.46 |
|
Everest |
6377.276 |
6356.075 |
300.80 |
|
Fischer 1960 |
6378.155 |
6356.773 |
298.30 |
|
International 1924 |
6378.388 |
6356.912 |
297.00 |
|
South American 1969 |
6378.160 |
6356.774 |
298.25 |
|
WGS 72 |
6378.135 |
6356.751 |
298.26 |
|
GRS 80 |
6378.137 |
6356.752 |
298.257 |
|
WGS 84 |
6378.137 |
6356.752 |
298.257 |
Ellipsoids and Ellipsoids
There about 20 ellipsoids in common use. Why are there so many ellipsoids when there is only one earth? The answer lies in the size of the earth and the problems in measuring any significant fraction of it. Basically in each region, Europe, North America, Africa, etc, surveys were analyzed to find the parameters of an ellipsoid that best fit that region.
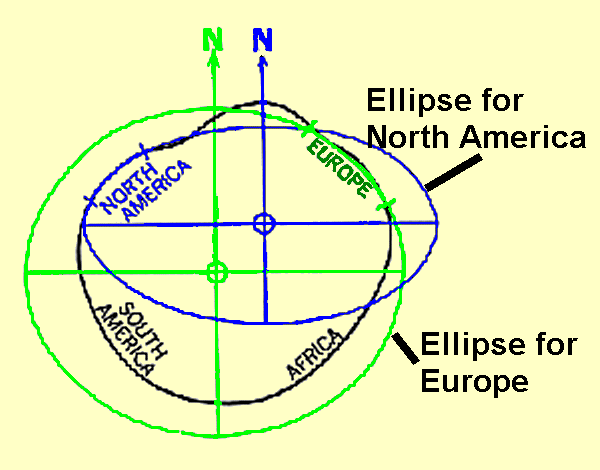
It was only in the 1960's with the introduction of satellite surveying that world wide measurements could be connected. Now we know that the assumption of an ellipsoid is very good. All the historical ellipsoids were fairly consistent. It is mainly the offset of the center that leads to map differences.
Satellite systems are particularly difficult to fit into this historical scheme of local models based on local measurements. This is because satellites exist above all this detail and respond to the large scale effects of the earth and its mass.
So, in order to make maps, or equipment that computes accurate positions from satellite systems we must know the ellipsoid used for the maps. Yes, but that is not the end of the story. While there may be a few ellipsoids in common use, maps also have local offsets/adjustment called datums. There are dozens of datums on each ellipsoid in common use. Next section, Datums.
|
|
||||
|
|
|
|
|
|